10_R assignament
Request
Distributions of the order statistics: look on the web for the most simple (but still rigorous) and clear derivations of the distributions, explaining in your own words the methods used.
Order statistics
Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference. In statistics we define the kth order statistic of a statistical sample as its kth-smallest value.[1]
Important special cases of the order statistics are the minimum and maximum value of a sample, and the sample median and other sample quantiles.
When using probability theory to analyze order statistics of random samples from a continuous distribution, the cumulative distribution function is used to reduce the analysis to the case of order statistics of the uniform distribution.
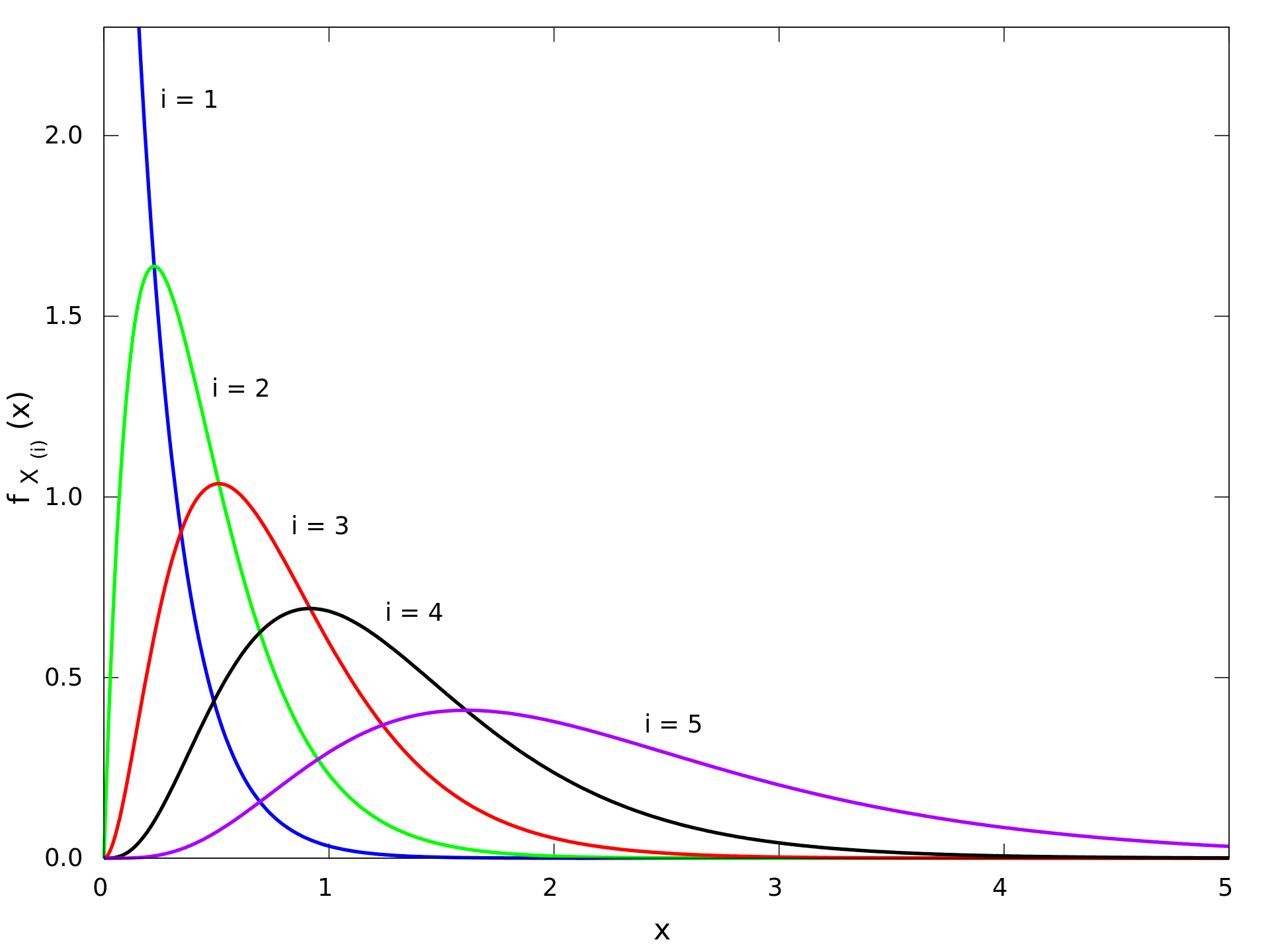
Probability density functions of the order statistics for a sample of size n = 5 from an exponential distribution with unit scale parameter
Distributions function of order statistic
For a random sample as above, with cumulative distribution Fx(x), the order statistics for that sample have cumulative distributions as follows (where r specifies which order statistic):
the corresponding probability density function may be derived from this result, and is found to be:
Moreover, there are two special cases, which have CDFs which are easy to compute.
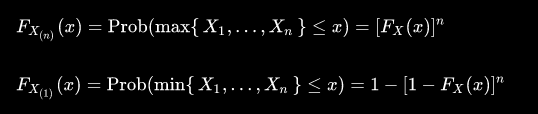
Which can be derived by careful consideration of probabilities.