13_R assignament

Request

An “analog” of the CLT for stochastic process: the standard Wiener process as “scaling limit” of a random walk and the functional CLT (Donsker theorem) or invariance principle. Explain the intuitive meaning of this result and how you have already illustrated the result in your homework.

Donsker’s theorem

In probability theory, Donsker’s theorem (also known as Donsker’s invariance principle, or the functional central limit theorem), named after Monroe D. Donsker, is a functional extension of the central limit theorem.[1 ]

Let X1,X2,X3… be a sequence of independent and identically distributed random variables with mean 0 and variance 1. and lets take S:= (Sn) where Sn is the sum of all Xi

The stochastic process S is known as a random walk. Define the diffusively rescaled random walk (partial-sum process) by:

The central limit theorem asserts that W^(n)(1) converges in distribution to a standard Gaussian random variable W(1) when n -> ∞.

Donsker’s invariance principle extends this convergence to the whole function W^(n):=hj(W^(n)(t) with t in 0,1

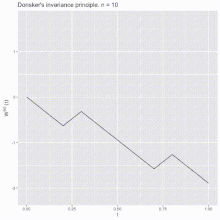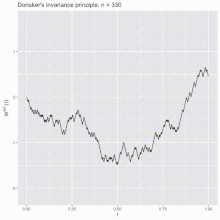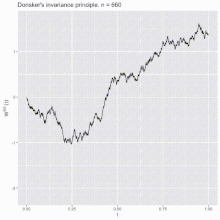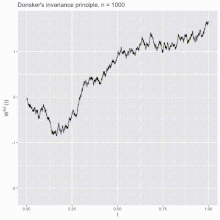
So Donkers’s theorem states that as random varabile taken values in a Skorokhod space the random function W^(n) converges in distribution to a standard Brownian motion for n -> ∞.(Donsker’s invariance principle). This concept is used among the other field for assets price inference [1]“url”,“https://en.wikipedia.org/wiki/Donsker%27s_theorem "